반응형
# Problem
|
n×m의 0, 1로 된 배열이 있다. 이 배열에서 1로 된 가장 큰 정사각형의 크기를 구하는 프로그램을 작성하시오. 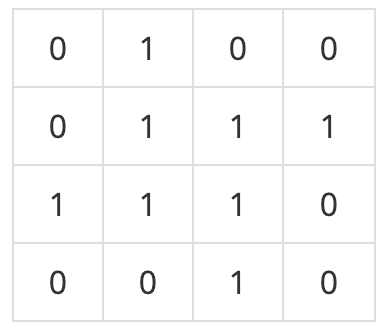 위와 같은 예제에서는 가운데의 2×2 배열이 가장 큰 정사각형이다. 입력첫째 줄에 n, m(1 ≤ n, m ≤ 1,000)이 주어진다. 다음 n개의 줄에는 m개의 숫자로 배열이 주어진다. 출력첫째 줄에 가장 큰 정사각형의 넓이를 출력한다.  |
# Solution
n,m = map(int,input().split())
a = [[0]*(m+1) for _ in range(n+1)]
dp = [[0]*(m+1) for _ in range(n+1)]
#dp[i][j] = i,j 까지 왔을 때, 가장 큰 정사각형의 한 변의 길이
#dp[i][j] = min(dp[i-1][j],dp[i-1][j-1],dp[i][j-1])+1
for i in range(n):
for idx,j in enumerate(list(map(int,input()))):
a[i+1][idx+1] = j
mx= 0
for i in range(1,n+1):
for j in range(1,m+1):
if a[i][j]:
dp[i][j] = min(dp[i-1][j],dp[i-1][j-1],dp[i][j-1])+1
mx = max(dp[i][j],mx)
print(max([max(i) for i in dp])**2)배열의 값이 1인 위치에 대해서
dp[i][j]는 i,j까지 왔을 떄 현재 위치를 포함한 가장 큰 정사각형의 한변의 길이
현재 값을 둘러 싸고 있는 위, 왼쪽, 왼쪽 위 대각선 중 최소값 + 1
배열의 값이 0 인 곳은 dp도 0
반응형
'Algorithm > 백준 알고리즘 풀이' 카테고리의 다른 글
| [Baekjoon] 16676. 근우의 다이어리 꾸미기 (0) | 2021.05.15 |
|---|---|
| [Baekjoon] 12849. 본대 산책 (DP) (0) | 2021.05.08 |
| [Baekjoon] 2167. 2차원 배열의 합 (DP) (0) | 2021.05.07 |
| [Baekjoon] 11055. 가장 큰 증가 부분 수열 (DP) (0) | 2021.05.07 |
| [Baekjoon] 1932. 정수 삼각형 (DP) (0) | 2021.05.07 |



