반응형
# Problem
Given the root of a Binary Search Tree (BST), return the minimum difference between the values of any two different nodes in the tree.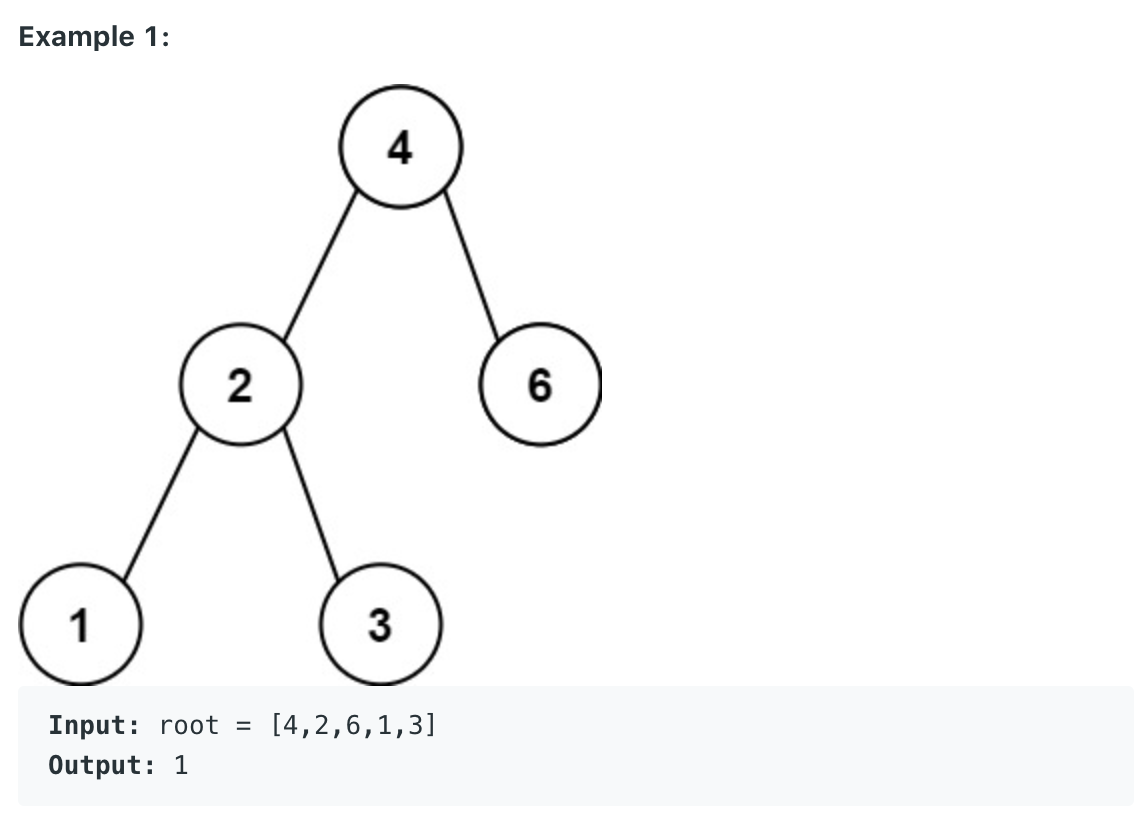  Constraints:
|
두 노드 간 값의 차이가 가장 작은 노드의 값의 차이 출력
# My Answer
class Solution:
md = 1e9 # 충분히 큰 값으로 설정
def minDiffInBST(self, root: TreeNode) -> int:
if root.left:
rt = root.left
while rt.right:
rt = rt.right
self.md = min(self.md,abs(root.val - rt.val))
self.md = min(self.md,self.minDiffInBST(root.left))
if root.right:
rt = root.right
while rt.left:
rt = rt.left
self.md = min(self.md,abs(root.val - rt.val))
self.md = min(self.md,self.minDiffInBST(root.right))
return self.md루트노드의 왼쪽 노드가 존재한다면
왼쪽 노드의 기장 오른쪽 노드와 루트노드와의 값의 차이가 가장 최소이고,
루트 노드의 오른쪽 노드가 존재한다면
오른쪽 노드의 가장 왼쪽 노드와 루트 노드와의 값이 차이가 가장 최소이다.
이 과정을 모든 노드에 대하여 반복하여 최소값을 찾는다.
# Solution 1 - 재귀 구조로 중위 순회
class Solution:
prev = -sys.maxsize
result = sys.maxsize
# 재귀 구조 중위 순회 비교 결과
def minDiffInBST(self, root: TreeNode) -> int:
if root.left:
self.minDiffInBST(root.left)
self.result = min(self.result, root.val - self.prev)
self.prev = root.val
if root.right:
self.minDiffInBST(root.right)
return self.result클래스 변수 result( 차이의 최소값) , prev ( 이전 순서 노드의 값 )
왼쪽 트리 - 부모 - 오른쪽 트리 중위 순회
바로 이전 값과의 차이 계산
# Solution 2 - 반복 구조로 중위 순회
class Solution:
def minDiffInBST(self, root: TreeNode) -> int:
prev = -sys.maxsize
result = sys.maxsize
stack = []
node = root
# 반복 구조 중위 순회 비교 결과
while stack or node:
while node:
stack.append(node)
node = node.left
node = stack.pop()
result = min(result, node.val - prev)
prev = node.val
node = node.right
return result스택 사용하여 DFS 풀이
위와 동일하게 왼쪽 - 부모 - 오른쪽 중위 순회
클래스 변수를 사용하지 않아도 된다
트리 순회
트리 순회란 그래프 순회의 한 형태로 트리 자료구조에서 각 노드를 정확히 한번 방문하는 과정
1. 전위 순회 (pre-order) NLR
현재 노드 - 왼쪽 - 오른쪽
2. 중위 순회 (in-order) LNR
왼쪽 - 현재 노드 - 오른쪽
3. 후위 순회 (post-order)LPN
왼쪽 - 오른쪽 - 현재 노드
반응형
'Algorithm > LEET CODE ( 파이썬 알고리즘 인터뷰)' 카테고리의 다른 글
| [LEET CODE] 215. Kth Largest Element in an Array (0) | 2021.05.26 |
|---|---|
| [LEET CODE] 105. Construct Binary Tree from Preorder and Inorder Traversal (0) | 2021.05.24 |
| [LEET CODE] 938. Range Sum of BST (0) | 2021.05.24 |
| [LEET CODE] 1038. Binary Search Tree to Greater Sum Tree (0) | 2021.05.24 |
| [LEET CODE] 108. Convert Sorted Array to Binary Search Tree (0) | 2021.05.19 |



